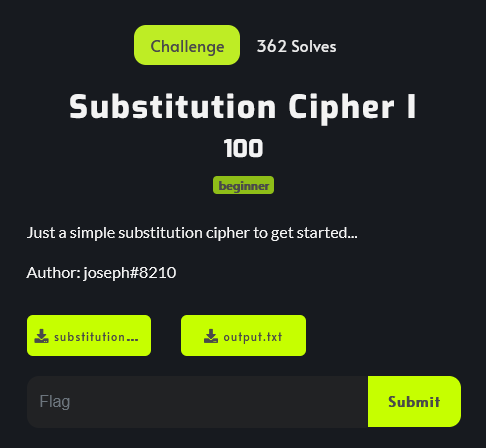Who knew I’d be writing a crypto writeup.

The Beginning

The challenge provides a SageMath bit of code, as well as a cipher text.

def encrypt(msg, f):
    return ''.join(chr(f.substitute(c)) for c in msg)

P.<x> = PolynomialRing(ZZ)
f = 13*x^2 + 3*x + 7

FLAG = open('./flag.txt', 'rb').read().strip()

enc = encrypt(FLAG, f)
print(enc)

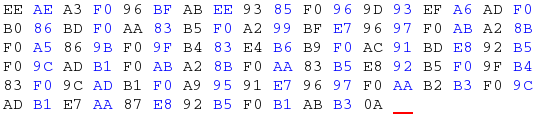That’s some messy looking cipher text…

Understanding the sage

Thankfully the SageMath here is nice and short. All that we need to know, is that each character of the flag is thrown into the encryption function f. So to reverse it, we just do the opposite.
Since the values were obtained by substituting each character into 13*x^2 + 3*x + 7, to get x back, we solve 13*x^2 + 3*x + 7 = <encrypted num>.

Neat-ify the cipher text

Those bytes looked a little unpleasant to me, so I decided to turn them into their appropriate unicode values.

txt = open("output.txt").read()
nums = []

for chr in txt:
    nums.append(ord(chr))

print(nums)

nums = [60323, 94187, 58565, 91987, 63917, 197053, 172277, 140927, 30103, 178315, 151963, 130307, 19897, 181373, 33973, 117617, 178315, 172277, 33973, 130307, 117617, 169297, 30103, 175283, 117617, 31367, 33973, 203507, 10]
Now that’s much better. Now to simply reverse the values and …

Oh no

An unnatural call

I then felt a disturbance in the air. My computer was absorbed by a bright, blinding light. When my senses recovered I saw this: I guess I have no choice now. The call of engineers can not be ignored.

An unholy solve

Matlab thankfully has a very simple way of solving quadratic equations. Using the root() function, in addition to rounding, I summoned the following code:

nums = [60323, 94187, 58565, 91987, 63917, 197053, 172277, 140927, 30103, 178315, 151963, 130307, 19897, 181373, 33973, 117617, 178315, 172277, 33973, 130307, 117617, 169297, 30103, 175283, 117617, 31367, 33973, 203507, 10];
results = "";
for i = 1:length(nums)
   results(i) = char(round(max(roots([13 3 (7-nums(i))]))));
end

sprintf("%s",results)

And just like that, the blinding light disappeared, and a flag emerged… DUCTF{sh0uld'v3_us3d_r0t_13}

What have I done…